Στόχος της εφαρμογής είναι να δείξει ότι το εμβαδό του τριγώνου διατηρείται το ίδιο ανεξάρτητα από το ύψος και την αντίστοιχη βάση που θα επιλέξουμε για τον υπολογισμό του. Γι αυτό δημιουργήσαμε ένα δυναμικό τρίγωνο που οι πλευρές του αλλάζουν μετακινώντας τις κορυφές του σε διάφορα σημεία.

Επιλέγουμε με τη σειρά τα τρίγωνα και στη συνέχεια το ύψος που αντιστοιχεί στην κορυφή του κάθε τριγώνου. Στη συνέχεια αλλάζουμε τις διαστάσεις των πλευρών του τριγώνου βάζοντας το ποντίκι μας στις κορυφές του τριγώνου και μετακινώντας τα σημεία.

Για να δείτε τη διαδραστική παρουσίαση για το εμβαδό του τριγώνου κάνετε κλικ στην παρακάτω εικόνα:

Για τους μαθητές αρκεί να έχουν μια βασική γνωριμία με τους υπολογιστές. Η δραστηριότητα είναι έτσι σχεδιασμένη έτσι ώστε τα πάντα να διαδραματίζονται σε μια οθόνη. Αυτό εξασφαλίζει τη δυνατότητα της εύκολης περιήγησης στη συγκεκριμμένη δραστηριότητα χωρίς να υπάρχει απώλεια προσανατολισμού που δημιουργείται από το άνοιγμα πολλών παραθύρων σε μια οθόνη.

Όσον αφορά τις προηγούμενες γνώσεις των μαθητών πρέπει πρώτα απ' όλα να έχουν κατανοήσει την έννοια της επιφάνειας και της καθέτου που χαράσσουμε σε μια ευθεία ή ένα ευθύγραμμο τμήμα και να γνωρίζουν τον τρόπο εύρεσης του εμβαδού του τετραγώνου και του παραλληλογράμμου.Επίσης να γνωρίζουν ποια είναι τα χαρακτηριστικά στοιχεία του τριγώνου και με ποιο τρόπο συμβολίζονται αυτά τα στοιχεία.

Σύμφωνα με το βιβλίο του μαθητή δύο ίσα τρίγωνα όταν ενώνονται με ένα συγκεκριμμένο τρόπο (αν τοποθετηθούν απέναντι οι δυο μεγαλύτερες πλευρές τους) τότε σχηματίζεται ένα παραλλήλόγραμμο. Συνεπώς το εμβαδό του τριγώνου είναι ίσο με το μισό του εμβαδού του παραλληλογράμμου που σχηματίζει. Σ'αυτή τη δραστηριότητα ακολουθείται ο ακριβώς αντίθετος τρόπος. Από ένα οποιοδήποτε τρίγωνο σχηματίζεται ένα ορθογώνιο παραλληλόγραμμο (αν φέρουμε κάθετες στη βάση του τριγώνου, προεκτείνουμε και στη συνέχεια φέρουμε κάθετη στη μία από τις κάθετες που φέραμε)και με τη λειτουργία της μεταφοράς και της περιστροφής τα δύο τρίγωνα που σχηματίζονται έχουν εμβαδό ίσο με το αρχικό τρίγωνο.Φυσικά ο ο τρόπος κατασκευής του δε γίνεται από τους μαθητές. Η κατασκευή παρουσιάζεται έτοιμη.Μπορεί σε αυτό το σημείο να γίνει μια συζήτηση για το σχήμα που προκύπτει από τις ιδιότητές του.

Οι στόχοι της δραστηριότητας είναι να βρουν με την καθοδήγηση του εκπαιδευτικού τον τρόπο εύρεσης του εμβαδού του τριγώνου.

Γι αυτό τον λόγο χρησιμοποιήθηκε το λογισμικό Geogebra που είναι ένα λογισμικό ανοιχτού τύπου, ένα δυναμικό και διαδραστικό λογισμικό Μαθηματικών και Γεωμετρίας. Επιλέχθηκε αυτό το λογισμικό γιατί οι μαθητές μπορούν να πειραματιστούν με τα εργαλεία του συγκεκριμένου λογισμικού ώστε να κατανοήσουν βασικές έννοιες και όρους της γεωμετρίας.Επίσης γιατί με αυτό το λογισμικό η κατασκευή διαφόρων γεωμετρικών σχημάτων γίνεται εύκολα και με ακρίβεια.Στη συγκεκριμμένη ενότητα κατασκευάστηκε ένα applet με τη βοήθεια του Geogebra.

Για την υλοποίηση της δραστηριότητας θα χρειαστούν 2 διδακτικές ώρες.

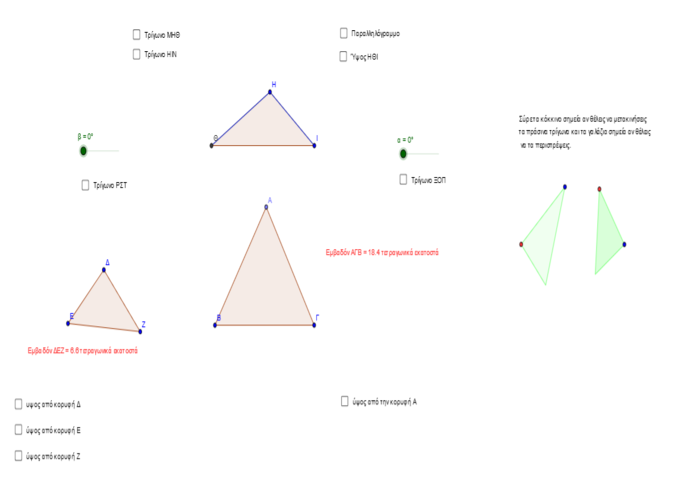
Ανοίγουμε την εφαρμογή κάνοντας κλικ στην παρακάτω εικόνα.Υπάρχουν τρία τρίγωνα, κάθε ένα εκ των οποίων αναφέρεται σε μία ξεχωρίστή δραστηριότητα που θα κάνουν οι μαθητές. Αρχίζοντας από το τρίγωνο ΔΕΖ ζητάμε από τους μαθητές να τοποθετήσουν τις κορυφές του τριγώνου σε διαφορετικό σημείο και να περιγράψουν τί αλλάζει κάθε φορά όσον αφορά την ταμπέλα του εμβαδού.Ο εκπαιδευτικός καλεί τους μαθητές να τραβήξουν τα ύψη από τις κορυφές του τριγώνου επιλέγοντας και αποεπιλέγοντας κατά περίπτωση τα αντίστοιχα κουτιά επιλογής.Δηλαδή κάθε φορά που αλλαζουν μια κορυφή επιλέγουν και το αντίστοιχο στην πλευρά που ανήκει η κορυφή, ύψος. Οι μαθητές πειραματιζόμενοι και ύστερα από συζήτηση βλέπουν ότι κάθε φορά που μετακινούν μία κορυφή του τριγώνου αλλάζει το μήκος των πλευρών του τριγώνου και το ύψος κι επομένως και το εμβαδό. Άρα το πρώτο συμπέρασμα που θα βγάλουν από αυτή την παρατήρηση είναι ότι το εμβαδό του τριγώνου εξαρτάται από το μήκος των πλευρών κι από το υψος γιατί αυτά είναι που αυξάνονται ή ελλατώνονται κάθε φορά που μετακινούμε τις κορυφές του τριγώνου.

Στη συνέχεια τους καλούμε να παρατηρήσουν το διπλανό τρίγωνο ΑΒΓ και να κάνουν το ίδιο. Παρατηρούν ότι από το τρίγωνο ΑΒΓ μπορούν να μετακινήσουν μόνο την κορυφή Α κατά οριζόντια φορά και σχηματίζοντας μια νοητή ευθεία που είναι παράλληλη προς την πλευρά ΒΓ. Ύστερα από συζήτηση βγάζουν το συμπέρασμα ότι η απόσταση του σημείου από το ευθύγραμμο τμήμα ΒΓ που είναι και συγχρόνως κάθετη σε αυτό είναι σταθερή και ότι το εμβαδό του τριγώνου παραμένει επίσης σταθερό.

Άρα αν συγκρίνουν τις παρατηρήσεις τους, οδηγούναι στο συμπέρασμα ότι σε ένα τρίγωνο που η βάση του ΒΓ είναι σταθερή και η κάθετη προς αυτό που είναι το ύψος του είναι κι αυτή σταθερή τότε τότε το εμβαδό του τριγώνου είναι κι αυτό σταθερό.

Ανάμεσα σε αυτές τις δύο συγκρίσεις και σε κάποιο σημείο ο εκπαιδευτικός τονίζει ότι ότι όταν στο τρίγωνο ΔΕΖ αλλάζουν οι κορυφές, τότε αλλάζουν και άλλα στοιχεία του τριγώνου κι ένα από αυτά είναι και το ύψος.

Άρα το εμβαδό του τριγώνου δεν αλλάζει όταν η βάση του και το ύψος του είναι σταθερά. Επομένως το εμβαδό του τριγώνου εξαρτάται από τη βάση και το ύψος του γιατί μόνο όταν αυτά τα δύο είναι σταθερά και μόνο τότε το εμβαδό μένει κι αυτό σταθερό. Για την καλύτερη κατανόηση των δυό δραστηριοτήτων μπορούμε να φτιάξουμε δύο πίνακες που να καταγράφουν τις παρατηρήσεις των μαθητών στα δύο τρίγωνα.

Πιθανές ερωτήσεις: Για το τρίγωνο ΔΕΖ.Τι αλλάζει κάθε φορά που μετακινούμε κάποια από τις κορυφές στο τρίγωνο ΔΕΖ. Τι αλλάζει επίσης. Τι συμπέρασμα βγάζουμε;

Για το τρίγωνο ΑΒΓ. Τι μπορούμε να μετακινήσουμε; Τι αλλάζει όταν μετακινούμε την κορυφή Α; Τι μένει σταθερό; Άρα από τι εξαρτάται το εμβαδό του τριγώνου;

Στη συνέχεια λέμε στους μαθητές ότι θα κάνουμε μια κατασκευή. Συγκεκριμμένα ότι θα κατασκευάσουμε ένα παραλληλόγραμμο με κοινή τη μία βάση του τριγώνου ΗΘΙ. Τους δίνουμε έτοιμη την κατασκευή καλώντας τους να τσεκάρουν το τετραγωνάκι που βρίσκεται δίπλα στη λέξη "παραλληλόγραμμο". Η κατασκευή ολοκληρώνεται. Οι μαθητές στη συνέχεια μπορούν να διακρίνουν όρισμένα στοιχεία της. Π.χ ότι τα ευθύγραμμα τμήματα ΜΘ και ΝΙ είναι κάθετα στη ΘΙ και ότι το μήκος τους είναι ίσο με το ύψος του αρχικού τριγώνου.

Αμέσως μετά τους καλούμε να παρατηρήσουν και να ονομάσουν τα νέα τρίγωνα που σχηματίζονται εκτός από το αρχικό. Τους λέμε να τα χρωματίσουν τσεκάροντας τα αντίστοιχα κουτάκια.Έχοντας κατασκευάσει εκ των προτέρων τα δύο πράσινα τρίγωνα στη δεξιά πλευρά καλούμε τους μαθητές να μεταφέρουν και να αποθέσουν τα δύο τρίγωνα στο παραλλήλόγραμμο ΜΝΘΙ. Παρατηρούν ότι τα δύο πράσινα τρίγωνα εφαρμόζουν ακριβώς στα τρίγωνα ΜΗΘ και ΗΝΙ. Στη συνέχεια τσεκάροντας τα κουτάκια στα τρίγωνα ΡΣΤ και ΞΟΠ μετακινούμε νοητά τα τρίγωνα πιο κάτω. Με την ίδια λειτουργία τα δύο πράσινα τρίγωνα εφαρμόζουν επίσης και στα τρίγωνα ΡΣΤ και ΞΟΠ. Αρα τα τρίγωνα που συγκρίναμε είναι ίσα. Μπορούμε στη συνέχεια να ξετσεκάρουμε τα κουτάκια στα τρίγωνα ΜΗΘ και ΗΙΝ για να μη μπερδευτούν από το σχήμα. Στη συνέχεια μετακινώντας τους δύο δρομείς α και β περιστρέφουμε τα δύο τρίγωνα. Ρωτάμε τι παρατηρούν. Το συμπέρασμα που βγάζουν είναι ότι όταν περιστρέφουμε τα δύο τρίγωνα τότε εφαρμόζουν ακριβώς στο αρχικό τρίγωνο. Άρα το εμβαδό των δύο τριγώνων είναι ίσο με το εμβαδό του αρχικού. Το εμβαδό όμως των τριών τριγώνων είναι ίσο με το εμβαδό του παραλληλογράμμου. Αφού το εμβαδό των δύο τριγώνων είναι ίσο με το εμβαδό του αρχικού το εμβαδό του αρχικού τριγώνου είναι ίσο με το μισό του εμβαδού του παραλληλογράμμου.

Επειδή δε, το εμβαδό του παραλληλογράμμου είναι ίσο με Βαση χ υψος τότε το εμβαδό του τριγώνου θα είναι ίσο με το μισό του εμβαδού του παραλληλογράμμου που γράφεται: Ε τριγ.= 1/2*β*υ.

Βρήκαμε επομένως με τι είναι ίσο το εμβαδό του τριγώνου στη γενική του μορφή.

Για να δείτε τη διαδραστική παρουσίαση για το εμβαδό του τριγώνου κάνετε κλικ στην παρακάτω εικόνα: